Demir ve Kehribardan Özel Göreliliğe V – Faraday Yasası

Bir önceki yazımda Hans Christian Ørsted’in elektrik akımı geçen bir kablonun, yakınındaki pusulanın ibresini saptırdığını bulmasından ve sonrasında André-Marie Ampère’in bu bulgudan hareketle formüle ettiği Ampère Yasası’ndan bahsetmiştim. Yazımda yer vermediğim önemli bir nokta, elektrik akımının pusulanın ibresini saptırmasının sadece “mucizevi bir olay” olarak görülmekle kalmaması, çok kullanışlı bir aletin icat edilmesine de vesile olmasıydı: galvanometre.

Yazımda pusula iğnesinin sapma açısından bahsederken aslında galvanometreye göz kırpmıştım. Eğer bir kablodan geçen elektrik akımı pusulanın iğnesini saptırıyorsa ve bu sapma açısı da geçen akımın “gücüne göre” değişiyorsa o zaman sapma açısına göre akımın ne kadar “güçlü” olduğunu ölçen bir “akım cetveli” tasarlayabiliriz. Ørsted’in bulgusundan hemen sonra geliştirilen bu aletin icadında Ampère’in de büyük bir payı vardı ve bu alete elektriğin ölü kurbağaların bacaklarını hareket ettirdiğini bulan İtalyan fizikçi Luigi Galvani’den esinlenerek galvanometre adını veren de oydu.

Ørsted’in elektrik akımının pusula ibresini saptırdığını bulmasından ve akabinde Ampère’in bu olguyu matematiksel bir formalizme sokmasından yaklaşık 10 yıl sonra, 1831 yılında, büyük İngiliz kimyacı ve fizikçi Michael Faraday görseldeki deney düzeneğini hazırlarken çok ilginç bir şey fark etti. Öyle ki, fark ettiği bu şey belki de modern toplumun inşasında rol alacak en önemli araçlardan biriydi. Bu müthiş buluşun ne olduğunu anlamak için görseldeki deney düzeneğini inceleyelim. Bu esnada sık sık deney düzeneğine bir kez daha bakmanızı tavsiye ederim.

Görselin en solunda akım kaynağımız yani pilimiz var. Tabii ki şemada pil olarak günümüzdeki pillere benzer bir görsel kullanılmış olsa da Faraday kendi yaptığı deneyinde önceki yazımda bahsettiğim voltaik pilleri, yani kimyasal pilleri kullanıyordu. Pilin pozitif kısmından çıkan kablo, demir bir halkanın sol tarafının etrafına sarılarak pilin negatif ucuna götürülüyor. Fakat henüz bu uca bağlanmıyor yani devre tamamlanmıyor, dolayısıyla elektrik akımı da henüz yok. Demir halkanın diğer ucuna yine aynı şekilde bir kablo sarılıyor fakat bu kablo bir pile değil bir galvanometreye bağlı. Yani eğer sağdaki kabloda bir şekilde bir akım oluşursa bu akım yukarıda bahsettiğim şekilde galvanometrenin ibresini hareket ettirecek. Peki ortadaki demir halka ne işe yarıyor? Yine önceki yazımda bahsettiğim üzere bir bobinden¹ geçen akım ile bir mıknatıs arasında Ampère’e göre bir fark yoktu. Faraday elektrik ve manyetik kuvvetleri “kuvvet çizgileri” dediği görünmez şeylerin ilettiğini düşünüyordu. Bu “kuvvet çizgilerinin” demir içinden geçerken demirin şeklini takip ettiğini daha önceden fark etmişti. Deney düzeneğine demir halkayı koymasının sebebi de soldaki bobinden geçen akımın oluşturacağı “kuvvet çizgilerini” demir boyunca iletmek ve sağdaki bobinin içinden geçirmekti.

Faraday, bu düzeneği hazırlayıp soldaki kabloyu pilin negatif ucuna taktığında ibre aniden hareket etti! Adeta biri ibreyi görünmez bir iple çok kısa bir süre çekip hemen bırakmış gibiydi. İbre bir süre iki tarafa salındı ve yavaşça sıfır noktasına geri döndü. İbre durduktan sonra kabloyu negatif uçtan çıkardı ve bu sefer ibre tam tersi yöne doğru gidip tekrar biraz salındıktan sonra sıfır noktasında durdu. Aslında benzer bir olguyu Ampère de gözlemlemiş fakat bunun deney aletlerinden kaynaklı bir hata olduğunu düşünmüştü. Fakat Faraday bunun böyle olduğunu düşünmedi, aksine deney düzeneğini daha da iyileştirdi. Daha uzun kablolar kullanarak sarım sayısını arttırdı ve daha güçlü piller kullandı. Deneylerinin sonunda galvanometrenin ibresinin sapma açısının kabloyu devreden koparma hızına bağlı olduğunu gözlemledi. Yani önemli olan soldaki kabloyu negatif uçtan mümkün olduğunca hızlı çıkarmaktı. Hatta bunu daha iyi gözlemlemek için soldaki kabloyu uçtan eliyle çıkarmak yerine çekiçle parçalamayı denedi. Bu şekilde ibrenin daha fazla saptığını gözlemledi.

Faraday’ın gözlemlediği bu olgu aslında değişen bir manyetik alanın akım yaratabilmesiydi. İbre üstündeki etki çok kısa süreliğineydi çünkü Faraday kabloyu taktıktan kısa bir süre sonra akım sabit bir hal alıyor ve dolayısıyla bobinin oluşturduğu manyetik alan da sabit kalıyordu. Ørsted’in gözlemlediği olguyu günümüz fiziği açısından değerlendirirsek, hareket eden elektrik yüklerinin manyetik alan oluşturması olarak düşünebiliriz. Faraday bu etkinin tam tersini gözlemlemiş ve göstermiş oldu. Bu buluş bugün kullandığımız birçok elektrik motorunun icat edilmesine olanak sağlayan temel prensipleri açıklıyordu. Hatta Faraday’ın bizzat kendisi de çok ilkel bir elektrik motoru yapmıştı. Bu deneyin benzer bir versiyonunu siz de evde tekrarlamak isterseniz ihtiyacınız olan malzemeler ve deneyin yapılışına dair kaynağı son notlar² kısmından bulabilirsiniz. Ayrıca Faraday’ın buluşlarıyla ilgili güzel bir kaynak olarak da bu³ videoya göz atabilirsiniz.

Bugün Faraday yasası olarak adlandırdığımız matematiksel formül Faraday’dan sonra formüle edilmiş olsa da buluşundan ötürü onun adını taşır. Peki Faraday Yasası nedir?

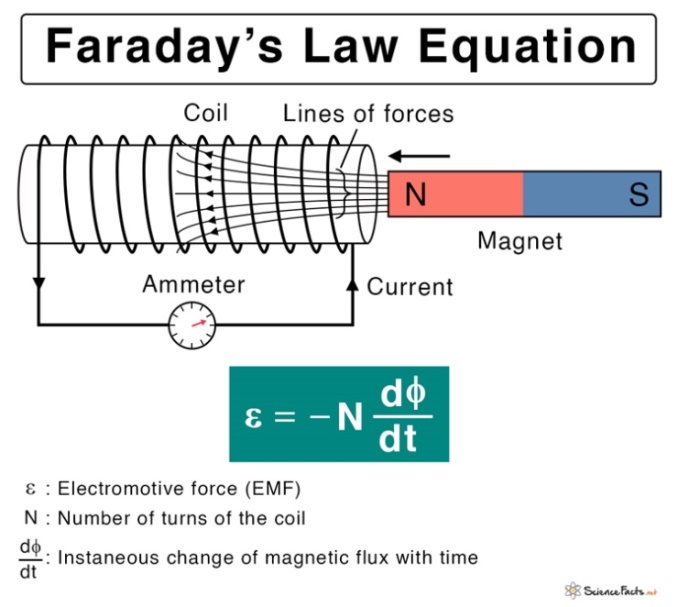
Faraday Yasası, bir yüzeyden geçen manyetik alandaki değişim ile o yüzeydeki iletkende oluşan akım arasında bir bağlantı kurar. Yukarıdaki görselde mıknatısın kuzey kutbu bobinin içine doğru yaklaştırılıyor. Dolayısıyla bobinin içinden geçen manyetik alan (Faraday’ın deyimiyle kuvvet çizgileri) miktarı artıyor. Devrede buna karşı koyacak şekilde bir elektrik akımı oluşuyor. Bu akımın yönünü bulmak için şu adımları uygulayabilirsiniz: sağ elinizin dört parmağını bardak tutar gibi sarın ve başparmağınızı havaya kaldırın. Manyetik alanın hangi yönde nasıl değiştiğine bakın. Bu örnekte manyetik alan bobinin sağından soluna doğru gidiyor ve mıknatıs yaklaştıkça bobinin içinden geçen manyetik alan miktarı artıyor. O zaman oluşan tepki akımının oluşturacağı manyetik alan, mıknatısınkine zıt yönde olmalı, yani başparmağınız sağ tarafı göstermeli. Sağ elinizi buna göre sararsanız şekilde gösterilen akım yönünü bulmuş olursunuz. Bu etki-tepki zıtlığını göstermek için formülün önünde bir eksi işareti var. “N” harfi sarım sayısını (ne kadar çok sarım o kadar fazla etki), Yunanca Φ harfi manyetik akıyı temsil ediyor. Formülde gördüğümüz üzere manyetik akıdaki değişim yani onun türevi (zamana göre değişimi) önemli. Eşitliğin en solundaki Yunanca epsilon harfi ise elektromotor kuvveti (ing: electromotive force) ifade ediyor. Bu terimi ilk kez duyduysanız endişelenmeyin. Aslında bu bir kuvvet değil, bildiğimiz potansiyel. Fakat o dönemde bu kavramlar daha net oturmamıştı ve elektriksel sıvıyı harekete geçiren bir tür kuvvet uygulayıcı güç fikri bu terimin adlandırılmasına neden olmuş.

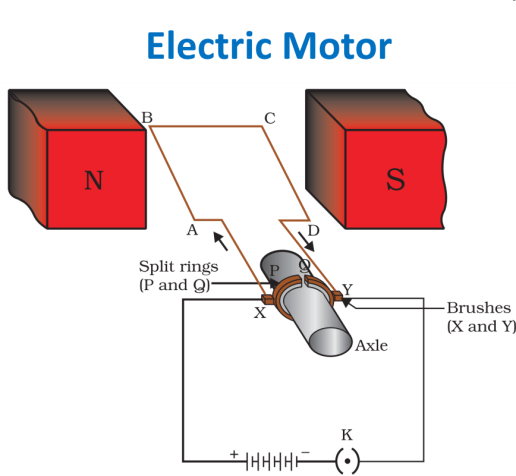
Peki elektrik motoru nasıl çalışıyor? Tabii ki günümüzde çok daha verimli ve karmaşık motorlar olsa da temel çalışma prensibini iyi açıkladığını düşündüğüm yukarıdaki görsele bakabilirsiniz. Çok güçlü bir mıknatısın kuzey ve güney kutupları arasına kare çerçeve şeklinde ABCD kablosu yerleştiriliyor. Bu kablo bir kuvvet yardımıyla (mesela rüzgâr veya akarsu sayesinde oluşan bir kuvvet yardımıyla) X-Y arasındaki mil (ing. axle) etrafında döndürülüyor. Çerçeve şekildeki gibi dururken içinden geçen manyetik akı minimum (sıfır), dikey dururken maksimum oluyor. Böylece hepimizin telefonlarımızı şarj ederken kullandığı prizlerimize alternatif akım sağlanıyor.

Böylece Maxwell denklemlerini oluşturan dört temel denklemimizi ve bunların tarihçesini görmüş olduk. Uzun bir yol aldık fakat sonraki yazılarımda bu uzun yolun hakkını vereceğini düşündüğüm birtakım gözlem, teori ve “paradokstan” bahsedeceğim. Bir sonraki yazımda Maxwell’in katkılarına ve bu katkıların doğurduğu sonuçlara göz atacağız.