Demir ve Kehribardan Özel Göreliliğe VI – Maxwell Denklemleri

Önceki yazılarımda elektrik ve manyetizmanın tarihini antik çağlardan alıp 19. yüzyıl ortalarına kadar getirmiş ve çeşitli denklemlerle tanışmıştık. 5 aylık uzun ve biraz meşakkatli bir yolculuğun sonunda en başından beri varmak istediğim noktaya gelmiş bulunuyoruz. Bu yazımdan itibaren günlük yaşantımızda görmeye alışık olmadığımız, kavraması zor birçok fikirle tanışacağız.

Fakat öncesinde size bir şey itiraf etmeliyim: sizlere biraz yalan söyledim! Olayların sırasını daha rahat anlaşılacağı şekilde verdim, aynı üniversite fizik-102 dersinin müfredatında olduğu gibi. Fakat asıl tarih benim anlattığım kadar düzgün ilerlemiyor. Örneğin Gauss Yasası’nı ele alalım. Gauss Yasası’nı ifade ederken elektrik ve manyetik alandan bahsetmiştik. Fakat manyetik alan ve elektrik alanı tarif ederken hayal ettiğimiz “kuvvet çizgileri” fikri Faraday ile geliyor, yani Gauss’tan sonra. Yasaların Gauss adını alma sebebi, vektör uzayları için denklemin matematiksel formunun genel kanıtını yapmasındandır. Yani o yasaları aslında Gauss keşfetmedi. Peki, bunları neden şimdi söylüyorum? Çünkü şimdi bahsedeceğim ismin yaptığı katkıların büyüklüğünü daha iyi ifade etmek istiyorum.

James Clerk Maxwell, 1831 doğumlu büyük İskoç matematikçi ve fizikçi. Kendisi sizlere beş ay boyunca anlattığım denklemleri düzgün matematiksel yapıya oturtan bir dâhidir. Öyle ki Maxwell’in denklemleri için “fizikteki ikinci büyük birleşim” diye bahsedilir. Birinci büyük birleşim Sir Isaac Newton’ın gökyüzündeki nesnelerin hareketiyle Dünya’daki yer çekimini kütle çekimi altında birleştirmesidir. Maxwell’e atfedilen birleşim ise elektrik, manyetizma ve ışık olgularının birleşimidir.

Maxwell Royal Institution’daki [Kraliyet Enstitüsü] derslere sık katılım gösterirdi. Burada ders veren Michael Faraday ile sık sık karşılaşırdı. Faraday o zamanlar biraz yaşlı olduğundan ikilinin arasındaki yaş farkından dolayı ilişkilerine çok samimi demek yanlış olsa da, Maxwell’in Faraday’a saygısı büyüktü. Maxwell, Faraday’ın “kuvvet çizgilerini”, yani bugünkü bakışımızla “alan” fikrini ciddiye aldı. 1861 yılında Fiziksel Kuvvet Çizgileri Üzerine isimli makalesinde, o ana kadar bilinen tüm olguları 20 bilinmeyenli 20 denkleme indirgedi. Hemen ertesi yıl bu denklemin vakum için çözümünden elektromanyetik alanın hızının ışığın hızına çok yakın olduğunu gösterdi.

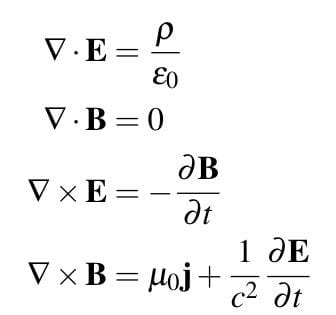
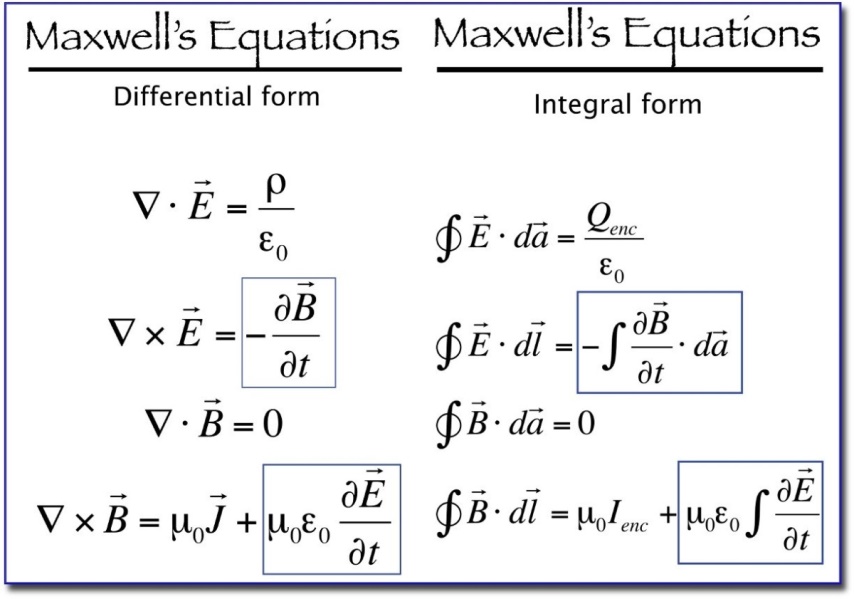
Bu noktada bir soluklanalım. Lisedeyken “Maxwell denklemlerinin vakum çözümü” veya “Einstein denklemlerinin karadelik çözümü” gibi ifadeler duyduğumda hep sinirlenirdim. Bir denklemin bir şey için çözümü olması da ne demek? Bunu Maxwell denklemlerinin bugün kullandığımız türü üzerinden açıklayayım. Bu denklemleri önceki yazılarımda bahsettiğim denklemlerle kıyaslamak ve benzerliklerini görebilmeniz için yazının en sonuna bir görsel bırakıyorum. Dilerseniz şu anda bakıp da devam edebilirsiniz.

Meşhur Maxwell denklemleri işte bu dört denklemdir. Daha önceki yazılarımda bahsettiğim denklemlere çok benzediğini fark edeceksiniz, yalnızca şu garip ters üçgen sembolleri var! Kısaca şöyle açıklayayım, bizim gördüğümüz denklemler “integral formdaydı” fakat yukarıdakiler “diferansiyel formda”. Bunun bizim için anlamı şu: yük, akım gibi kavramlar yerine yük yoğunluğu, akım yoğunluğu gibi kavramlar var. Fakat fikir aynı ve bizim gördüğümüz denklemlerle tamamen eşler.

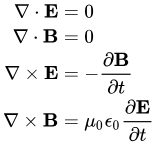
Peki, ne demek bu denklemleri vakum için çözmek? Çok basit. Vakumda herhangi bir nokta alalım. Buradaki yük yoğunluğu ve akım yoğunluğu nedir? Sıfır! Vakumun tanımı icabı içinde hiçbir madde yok, dolayısıyla yük de yok. Yukarıdaki denklemde yük yoğunluğu ve akım yoğunluğu yerine sıfır yazarsak aşağıdaki hali alır.

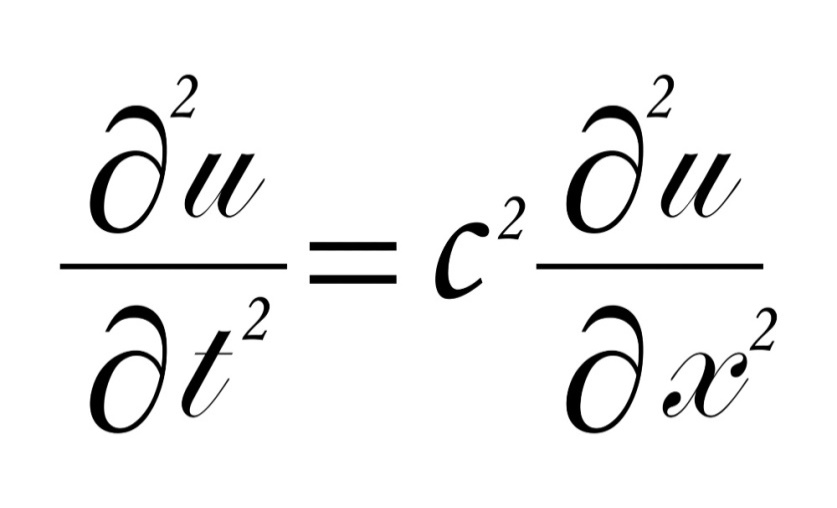
Bu denklemi elektrik alan veya manyetik alan için çözebilirsiniz. Her ikisi için de şu türden bir çözüm geliyor.

Bu bir dalga denklemidir, yani dalgaları ifade eden denklem. Buradaki c harfi dalganın hızı. İşte Maxwell denklemlerini vakum için çözdüğünde ışığın hızı için şöyle bir şeyle karşılaştı:

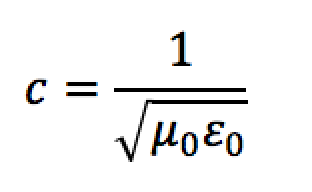
Bu garip Yunan harflerini hatırladınız mı? Size daha önceki yazılarımda bu sabitlerin önemli olacağını söylemiştim! Bu sabitler sırasıyla vakumun manyetik geçirgenliği ve elektrik geçirgenliği katsayıları. Maxwell’in zamanında bu sabitlerin değeri yaklaşık olarak biliniyordu. Bunları yerine koyduğunda elektrik ve manyetik alanların hızını 310.740.000 metre/saniye olarak hesapladı. Bu sayının ışığın o zamanki ölçülen hızına çok yakın olduğunu anında fark etti ve ekledi : “Sonuç gösteriyor ki ışık ve elektromanyetizma aynı maddenin etkileridir ve ışık elektromanyetik yasalara tabiidir”.ⁱ

Burada hemen dikkatinizi çekebilecek başka bir nokta daha var: ışığın hızını belirleyen terimler sabit! Dolayısıyla ışığın hızı da sabit. Aha! Özel göreliliği bulduk mu sonunda yoksa? Maalesef heyecanınıza mani olmak durumundayım. Bir hızdan bahsederken her zaman şu soruyu sormalısınız: peki ama bu hız kime göre? Daha iyi açıklamak için kısaca su dalgalarına bakalım.

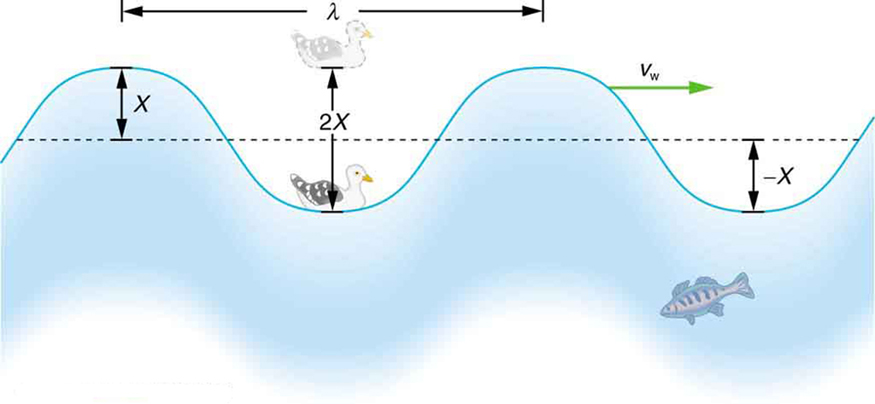
Yukarıda dalga denklemi olarak bahsettiğim denklem tüm dalgalar için kullanılan genel bir denklemdir. Bahsettiğimiz dalga her neyse onun hızını ifade eden c terimi dalganın yayıldığı ortama göre hızını ifade eder. Neticede dalga dediğimiz şey her zaman bir ortamda yayılır. Su dalgasının hareketiyle futbol tribünlerindeki Meksika dalgası tamamen eş şeylerdir. Meksika dalgasında sırası gelen insanlar ayağa kalkıp oturur. Stadyumun etrafında koşuşturmazlar. Su dalgaları da aynı şekilde ilerler, sırası gelen su “ayağa kalkıp oturur”. Meksika dalgasını bilmeyenler için bir video linki bırakıyorum.² Bu dalganın hızı tamamen insanların oturup kalkma hızına bağlıdır, yani yayıldığı ortama.

Dolayısıyla Maxwell ışığın hızını sabit bulduğu için hiç de şaşırmamış olsa gerek. Çünkü bilinen tüm dalgaların hızı yayıldığı ortama göre sabittir. Ancak yukarıdaki görseldeki balığı düşünelim. Balık dalgalara karşı yüzerken yukarı baktığında su dalgasının daha hızlı gittiğini söyleyecektir. Yani suya göre hareket eden gözlemciler için doğal olarak dalganın hızı değişecektir. Dolayısıyla Maxwell de ışığın içinde ilerlediği teorik madde olan etere göre hızının sabit olduğunu düşünüyordu.

Nitekim o yıllarda ve ilerleyen yıllarda eteri bulmak için çeşitli deneyler yapıldı. Bunlardan sonraki yazımda detaylıca bahsedeceğim. Fakat deneylerden pek de hoş sonuçlar gelmiyordu. Fizikte devasa bir krizin eşiğine gelinmişti. İşte her kriz ortamında olduğu gibi bu krizde de kurtarıcı bir kahraman gerekiyordu.

Önceki yazılarımda gördüğümüz denklemler sağ taraf, aynı denklemlerin diferansiyel formları sol taraf olmak üzere açıklayıcı bir görsel.