Bir önceki yazımda elektrik alan için Gauss yasasına bakmıştık. Gauss yasası bir yüzeyden geçen elektrik alan ve yüzey içindeki toplam yük ile ilgili bir ilişkiyi bize söylüyordu. Peki benzer bir yasa manyetizma için de var mı?
İlk yazımda manyetizmanın tarihinden bahsederken değindiğim çok önemli bir dönüm noktası Fransız Peter Pelerin de Maricourt’un bir mıknatısın ikiye bölündüğünde iki ayrı mıknatıs olduğunu yazmasıydı. Yani bir mıknatısın kuzey ve güney kutbu olduğunu gören Maricourt, bunları ayırmayı amaçladığında bunu başaramadı. Aslında Maricourt’un gözlemlediği şey manyetik monopollerin (tekkutup) olmamasından başka bir şey değildi. Peki, bu tam olarak ne demek?
Örneğin, uçlarına iletken metal küreler taktığımız iki çubuk düşünelim. Elbette çubukları tuttuğumuz tutamaçlar yalıtkan malzemeyle kaplı olsun ki yük üstümüzden kaçamasın. Bu iki küre nötr olsun; yani içlerindeki negatif ve pozitif yük miktarı birbirine eşit olsun, ve küreleri birbirine değdirelim. Daha sonra + yüklü olduğunu bildiğimiz üçüncü bir küreyi, yan odadan laboratuvarımıza sokalım ve bu iki küreden soldakine yaklaştıralım fakat değdirmeyelim. Negatif yükler, yani elektronlar, yaklaştırdığımız pozitif yüklerin çekim etkisiyle soldaki küreye hareket etmeye başlayacak ve orada yığılacaklar. Bunun sonucu olarak sol küre negatif yüklenirken sağdaki küre de eşit oranda pozitif yüklenecek. Şimdi aniden en baştan beri birbirine değdirdiğimiz bu iki küreyi ayıralım. Artık nur topu gibi iki evladımız var, biri negatif biri pozitif yüklü. Bu kürelerden biri için, mesela pozitif yüklü olan için, Gauss denklemini yazacak olursak kürenin net yük miktarı pozitif olduğu için dışarı yönlü elektrik alan çizgileri oluşturduğunu bulacağız. Bu sonuç pek de şaşırtıcı değil, zira zaten en başta pozitif ve negatif yüklerin varlığından hareket ettik. Yani elektrik monopollerinin varlığını varsaydık.
Bu sonuç pek de etkileyici olmadı. Bir de şu şekilde deneyelim:
Benjamin Franklin’in elektriğin ikili doğası olduğunu yazmasından önce yaşayan bir bilim insanı olduğunuzu hayal edin. Elinizde bir cam tüp ve bir de kumaş var. Kumaşı cama sürttünüz ve camı ortasından yatay duracak şekilde bir ipe bağladınız. Elinize başka bir cam tüp aldınız ve önceki sürttüğünüz kumaştan başka bir kumaşı tüpe sürttünüz. İkinci cam tüpü ipte asılı duran cam tüpe yavaşça yaklaştırdınız. İpte asılı duran cam tüpün adeta diğerinden kaçmak istercesine, yüce Newton’ın yerçekimine rağmen yaklaştırdığınız tüpten uzaklaştığınızı gözlemlediniz. Sonra önceki kullandığınız kumaşlardan birini yaklaştırdınız ve bu sefer de tam tersine adeta birbirlerine gitmek istediklerini gözlemlediniz. Aklınıza küçükken evinizin önünde bulduğunuz ve bir tarafı diğerinin bir tarafını çekerken diğer tarafı aynı tarafı iten sihirli taşları hatırladınız. Ancak bu sefer sanki bu taşların farklı davranan iki yarısını ayırmışlar da ayrı ayrı kullanabiliyorsunuz gibi bir etki gözlemlediniz. Sanki bu elektrik denen sihirli şeyi sağlayan iki türden şey var (Franklin bunlara elektriksel sıvı demişti) ve bunlar kendi başlarına bir yerden bir yere hareket edebiliyor. Bugün biliyoruz ki bunu sağlayan proton (+) ve elektron (-) denen birim yükler var.
Ancak manyetizma için benzer bir strateji uygulayamıyoruz. Çünkü Maricourt’un da gördüğü gibi, bir mıknatısı ikiye böldüğümüzde, yine ikişer kutuplu iki ayrı mıknatıs elde ediyoruz. Ayrıca bu mıknatısların kuzey ve güney kutuplarının manyetik akıları da birbirine eşit, yani mıknatısın toplam manyetik akısı sıfır! Manyetik monopol olmaması da, elektron veya proton gibi kendi başlarına var olan manyetik yüklerin olmaması anlamına geliyor.
İ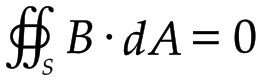
şte elektrik alan için olan Gauss yasasını manyetizmaya uyguladığımızda ortaya şöyle bir şey çıkıyor:
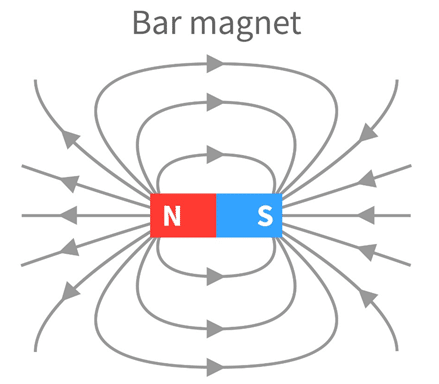
Hatırlarsanız elektrik alan için olan formülde sol tarafta toplam akı varken sağ tarafta içerideki yük miktarı vardı. Burada sağ tarafta sıfır olması aslında bize manyetik monopoller yoktur demiş oluyor. Diğer bir bakış açısıyla, evrende hangi noktanın etrafına hayali bir şekil çizerseniz çizin şekle giren ve çıkan manyetik akının toplamı sıfır olacaktır. Çizdiğiniz şeklin, mesela küre olsun, her yerinden dışarıya çıkan elektrik alan okları gibi bir örnek manyetizma için söz konusu değil. Manyetik alan çizgileri hep kendi üstüne kapanıyor, bu nedenle de hayali küremize giren ve çıkan manyetik alan çizgi miktarı sıfır oluyor. Daha iyi anlaşılabilmesi için görseldeki manyetik alan çizgilerini inceleyebilir, şeklin istediğiniz kısmına hayali bir kapalı yüzey (örneğin bir küp) çizerek şekle giren ve çıkan manyetik akıya bakabilirsiniz.
Bu yazıda bahsettiğimiz manyetik alan için Gauss Yasası, Maxwell denklemlerinden ikincisini oluşturacak ve özel göreliliğe gittiğimiz yolda bir adım daha atmamızı sağlayacak.
Yazıya son vermeden önce manyetik monopollerin varlığıyla ilgili güncel tartışmalardan bir kesit sunmak isterim. Kuantum mekaniğinin doğduğu ve geliştiği yıllarda çok önemli bir isim olan İngiliz fizikçi Paul Dirac, 1931 yılında bir makale yayınladı. Elektrik yükünün neden kuantize (parça parça, tekli) olduğuna cevap olarak bu makalede eğer manyetik monopoller varsa evrendeki tüm elektrik yüklerinin kuantize bir şekilde var olması gerektiğini gösterdi. Bu çok önemli bir adım olup manyetik monopollerin var olma olasılığı hakkında umut verici bir haber olsa da onların varlığını kanıtlamıyor. Bu makalenin yayınlanmasından beri manyetik monopol bulma araştırmaları hala sürmekte. Bilim insanları eğer böyle bir parçacık varsa kütlesinin diğer parçacıklara göre çok daha yüksek olması gerektiğini söylüyor. Bu da proton veya nötron gibi kütlesi görece daha küçük olan parçacıkları gözlemlememiz için ulaşmamız gereken enerji seviyesinin çok daha üstüne çıkmamız gerektiğini söylüyor. Nitekim, CERN’deki ATLAS deneylerinde bu enerji seviyelerine çıkılmaya çalışılıyor1.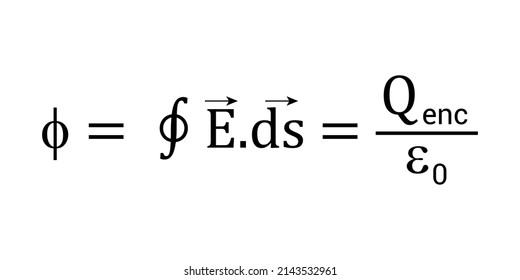
Son olarak önceki yazıda elektrik alan için Gauss Yasası yazıda gözükmediği için aşağıya görsel olarak bırakıyorum.
1 https://home.web.cern.ch/news/news/physics/quest-curious-magnetic-monopole-continues
