Demir ve Kehribardan Özel Göreliliğe IV – Ampère Yasası

Alessandra Volta’nın voltaik pili icat etmesinden yaklaşık 20 yıl sonra, 1820 yılında bir kış günüydü. Danimarkalı fizikçi Hans Christian Ørsted derslerde kullanmak için voltaik pilli bir devre hazırlıyordu. Rivayet odur ki şans eseri o sırada devreyi tamamlayan kablonun hemen altında bir pusula duruyordu. Ørsted kabloyu pilin diğer ucuna bağlayıp devreyi tamamladığında çok ilginç bir olay oldu. Pusulanın Dünya’nın kuzeyini gösteren kırmızı ucu bir anda sapmaya ve farklı bir yönü göstermeye başladı! Olan biteni daha iyi anlamak isteyen Ørsted, kablonun masanın üzerinden geçen kısmını düzleştirdi ve pusulanın kırmızı ucunu kabloyla aynı hizaya gelecek şekilde hizaladı. Kablonun ucunu pilin diğer ucuna taktı ve aynı şeyi bir daha gözlemledi. Birkaç dakika süren şoktan sonra (bu kısım bizim hayal gücümüzün ürünü olsun) bir bilim insanı olarak kalitesini gösterdi ve pusulanın kablodan uzaklığını adım adım artırarak her bir uzaklık için kaç derece saptığını not aldı. Fakat gördüklerinin sıra dışılığından olsa gerek bu bulgusunu yayınlamak üzere bir bilimsel dergiye başvurmadı¹. Çağın önde gelen birkaç bilim insanına mektup yazarak gözlemlerini ve notlarını aktardı. Ancak bu büyük olay hemen bilim çevreleri arasında yayılmaya başladı.

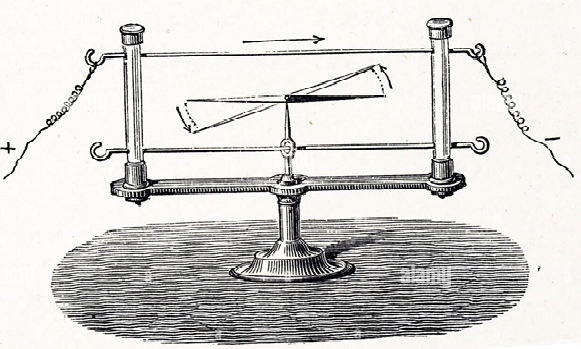
Bu noktada durup bir soluklanalım ve bu bulgunun neden bu kadar sıra dışı olduğu hakkında düşünelim. Gözlerimizi kapayalım ve kendimizi Ørsted’in büyük keşfini yaptığı uzay-zaman koordinatlarına ışınlayalım. Ørsted’i rahatsız etmeden (orada olduğumuzu anlarsa ürkebilir) masanın üzerine gerilmiş kabloya yaklaşalım ve kablonun tam üstünden aşağıya bakalım. Masanın altında duran pusulanın kuzeyi bize göre yukarıya (+y ekseni) bakıyor olacak. Şimdi Ørsted’in devreyi bağlamasını bekleyelim ve pusulanın kuzey kutbunu gözlemleyelim. Devre bağlandığı anda pusulanın kırmızı ucu (yani kuzey kutbu) sola doğru (-x ekseni) hareket etmeye başladı. Biraz ileri geri sallandıktan sonra belli bir açıyla (yaklaşık +y ekseniyle 45 derece yapacak şekilde olsun) durdu. Öncelikle aklımıza şu soru gelmeli: neden sol? Pusulanın iğnesi bir şekilde kabloya doğru, yani suratımıza doğru (+z yönü) çekilse bu kadar şaşırtıcı olmazdı. Nitekim doğada böyle etkiyen en az üç kuvvet olduğunu Ørsted de biz de biliyoruz: kütleler birbirlerini birbirlerine doğru çekiyor, iki yük arasındaki elektrik kuvveti ve iki magnet arasındaki manyetik kuvvet de böyle davranıyor. Fakat pusula iğnesi kabloya doğru değil, yani kabloyla pusula iğnesinin oluşturduğu düzlemde değil de başka bir düzlemde, sola doğru hareket ediyor. Bu bir simetri kırınımı değil midir? Doğa neden sağ ve soldan birini tercih etsin ki? İkinci bir soru da şu olabilir: burada etkiyen kuvvet ne kuvveti? Elektrik kuvvetiyse nasıl oluyor da sadece manyetik kuvvetten etkilendiği görülen nötr bir cisme etki ediyor? Belki de kablodaki “elektriksel sıvı” aynı zamanda “manyetik bir sıvıdır”.

Benzer nedenlerle, özellikle de simetri kırınımı argümanı nedeniyle, Jean Dominique Arago Paris’teki bilimler akademisine Ørsted’in bu bulgusunu sunduğunda bilim çevreleri pek güvenilir bulmamıştı. Fakat sunumdan birkaç hafta sonra Arago aynı zümrenin karşısında deneyi tekrarlayarak şüpheye yer bırakmadı. Fransız fizikçi André-Marie Ampère, Ørsted’in bu bulgusunu ilk duyduğunda ona inanmıştı². Sonrasında Arago’nun deney tekrarını da bizzat gördü. Bu bulguyu duyar duymaz üzerine düşünmeye başladı. Ampère o ana kadar bilinen tüm manyetik etkilerin ve Ørsted’in gözlemlediği etkinin akım nedeniyle olduğunu düşünüyordu. Ampère’in bu teorisine göre hem Dünya’nın hem de magnetlerin içerisinde elektrik akımı olması gerekiyordu. Ampère’e göre “manyetik etki” denilen tüm etkiler elektrik akımı ile açıklanabilir olmalıydı. Bu hipotezle Ampère tüm bu etkileri tek bir açıklamada birleştirmeyi amaçlıyordu. Dahası, Ampère bu hipotezi sayesinde daha önce hiç gözlemlenmemiş bir olguyu da tahmin edebilmişti: akım taşıyan iki kablo arasındaki kuvveti.

Takvimler 1822’yi gösterdiğinde Ampère teorisini matematiksel bir zemine oturtmuştu. 1826 yılında Mémoire sur la théorie mathématique des phénomènes électrodynamiques, uniquement déduite de l’experience³ kitabında bu çalışmalarını yayınladı. Buradaki “elektrodinamik” (Fr. électrodynamiques) sözcüğüne dikkat çekmek isterim. Ørsted akım taşıyan kablo ile pusula arasındaki etkileşimi tarif etmek için “elektromanyetik” ve “elektromanyetizma” kelimelerini türetmiş ve gözlemlerini aktarırken bu kelimeleri kullanmıştı. Ampère de akım taşıyan iki kablo arasındaki kuvvet ile birbirine göre duran iki yük arasındaki elektrik kuvvetini birbirinden ayırmak için “elektrodinamik” (hareket eden yükler için) ve “elektrostatik” (birbirine göre durgun yükler için) kelimelerini türetti ve ilk kez bu kitapta kullandı.

Bu uzun fakat heyecanlı tarihçeden sonra bir de işin matematiğine bakalım. Fakat matematiğe geçmeden hemen önce belirtmeliyim ki aşağıda bahsedeceğimiz denklem Ampère’in orijinal denklemi değil. Bizim amaçlarımız açısından önemli bir fark yaratmadığı, daha basit ve anlaşılır olduğu için bu formunu kullanmayı tercih ettim.

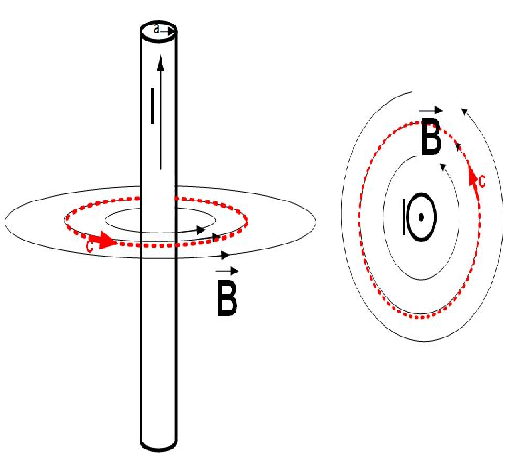Ampère Yasası, kapalı bir yolun içinden yüzeye dik şekilde geçen akım ile oluşan manyetik alan arasında bir ilişki kuruyor. Görselde gösterilen kırmızı yolun üzerinde çok küçük bir uzunluk seçelim ve tam o noktadaki manyetik alanla bu uzunluğu çarpalım. Bu çarpım aslında vektörel bir çarpım olduğu için seçtiğimiz minik uzunlukla manyetik alanın birbirine göre yönelimi bu çarpımın sonucunu değiştirecektir fakat yukarıdaki görsel özelinde çizdiğimiz şekil bir çember olduğu ve manyetik alan her noktada çembere teğet olduğu için vektörel çarpıma odaklanmamıza gerek yok. Manyetik alanla seçtiğimiz minik uzunluğu direkt çarpabiliriz. Bu şekilde minik uzunluklar seçerek her bir minik uzunluğu üstündeki manyetik alanla çarpıp bulduğumuz değerleri topluyoruz. Başladığımız yere dönene kadar yani kapalı bir yol çizene kadar bunu yapıyoruz. Bu toplam bize ortamın manyetik geçirgenlik katsayısıyla çizdiğimiz yolun içinden ona dik geçen akım miktarının çarpımını veriyor. Anlatması biraz karışık dursa da görseli biraz inceleyerek rahatça anlaşılabileceğini umuyorum.

Burada önemli bir nokta da akımın hangi yönde seçileceği. Örneğin görselde yukarı yönle ve I harfiyle gösterilen akım pekâlâ aşağı yönlü de olsa çizdiğimiz yola dik olacaktı. Burada belki liseden de hatırlayacağınız sağ el kuralını kullanıyoruz: Sağ elinizin baş parmağı hariç dört parmağını çizdiğiniz yolu hangi yönde çizdiyseniz o şekilde sarın ve baş parmağınızı havaya kaldırıp hangi yönü gösterdiğine bakın. Yukarıdaki örnekte bu yön yukarı olacaktır.

Peki ama neden sağ el? Bunu ileriki yazılarımdan birinde detaylıca ele almak istediğimden burada çok uzunca değinmeyeceğim. Ancak kısaca bahsetmek gerekirse hem manyetik alanı hem de manyetik kuvveti bulurken sağ el kuralını kullandığımız için, yani iki kere kullandığımız için çıkan sonucun yönü hangi eli kullandığımızdan bağımsız oluyor. Pekâlâ solak bir uzaylı da sol el kuralıyla aynı sonucu bulabilir. Sonuçtan kastım kuvvet, ivme gibi fiziksel önemi alan büyüklükler. Fakat aynı uzaylıyla manyetik alanın yönü konusunda anlaşamayabilirdik. Ancak bu konuyu ileriki yazılarımdan birinde daha detaylıca ele almak istediğimden şimdilik burada bırakıyorum.

Böylece Maxwell denklemlerinin üçüncüsü olan Ampère yasasını bu yazıda ele aldık. Artık Maxwell denklemlerini tamamlamaya sadece bir adım, özel görelilikten bahsetmeye ise sadece iki adım uzaklıktayız.