Demir ve Kehribardan Özel Göreliliğe VII – Işık Saçan Eter

Bir önceki yazımda o güne kadar gördüğümüz tüm denklemleri matematiksel olarak geliştiren ve toparlayan Maxwell denklemlerinden bahsetmiş ve sonraki yazım için özel göreliliğe göz kırpmıştım. Fakat Einstein ve özel göreliliğe gelmeden önce eterin kısa tarihinden ve neden bu kadar önemli olduğundan bahsetmezsem bunun can alıcı bir hata olacağının farkına vardım. Çünkü iki rakip bilimsel teori arasından hangisini seçeceğimizi belirlerken kullandığımız Ockham’ın usturasıⁱ ilkesinin bilim tarihindeki önemli örneklerinden biri de Einstein’ın etere getirdiği bakış açısıdır. Bu nedenle sizleri yormayacak şekilde bir eter tarihçesi sunmayı uygun buldum. (Hatta bunu bir ara bölüm gibi düşünüp başlığı VI.I yapmaktan kendimi son anda alabildim.)

Peki, nedir bu eter ve neden bu kadar önemli? Maxwell denklemlerinin çözümünün bir dalga denklemi çözümü olduğundan ve bilinen tüm dalgaların yayılacakları bir ortama ihtiyaç duyduğundan bahsetmiştim. Eter, diğer adıyla ışık saçan eter [ing. luminiferous ether], ışığın içinde yayıldığı düşünülen hayali ortamdır. Neden hayali dediğim ilerleyen paragraflarda anlaşılacaktır. Işık saçan eter denme sebebi de tarihte birçok şeyi açıklamak için kullanılan diğer eterlerden ayırmak. Geçmişte insanlar nöronlarımız arası sinirsel iletimin bile yayıldığı ayrı bir eter olduğunu düşünmüşler.

Işık saçan eter fikri eski bir kavram. Birçoğumuz Sir Isaac Newton’ı kütle çekim teorisiyle bilsek de kendisi optik alanında da önemli çalışmalar yapmıştır. Newton ışığın küçük mermi benzeri parçacıklardan oluştuğunu düşünüyordu. Böyle düşünmesinin nedenlerinden biri de İzlanda taşıydı. O dönemlerde (17.yy) bulunan İzlanda taşı bilim camiasında büyük bir etki yaratmıştı. Çünkü daha önceden bilinmeyen çok ilginç bir özelliği vardı: çiftkırılım.

Newton’ın mermi ışık teorisi bu ilginç özelliği açıklamakta çok başarılıydı. Ama ışığın kırılım [ing. refraction] ve dağılımını [ing. diffraction] açıklamakta başarısızdı. Newton’ın çağdaşlarından Christiaan Huygens ise ışığın boyuna dalga² [ing. longitudinal wave] olduğunu düşünüyordu. Eterin bildiğimiz maddeden çok daha küçük kürelerden oluştuğunu ve ışığın bu ortamda yayılan bir dalga (top havuzunda bir dalga gibi) olduğunu savundu. Bu görüşü kırınım ve dağılımı açıklamada başarılı olsa da çiftkırılımı açıklamada o kadar başarılı değildi. Isaac Newton’ın o günlerdeki gücü ve statüsünün de etkisiyle ışığın parçacık/mermi teorisi bilim çevrelerinde kabul görmüştü.

Işığın mermi teorisi sonraki yüzyılda darbeler almaya başladı. 1800’lerin başında Thomas Young ve Jean Fresnel ışığın enine bir dalga [ing. transverse wave] olabileceğini ileri sürdü. Bu şekilde çiftkırılımı da açıklayabilirdi. Fakat böyle bir ışığın içinde ilerleyeceği eter Huygens’in eterine benzese de bir farkı vardı: sıvı değil katı olması gerekti. Madde ile etkileşmeyen (günlük hayatta hiçbir şekilde hissetmediğimiz) bir katı eter fikri absürttü! Bunu açıklamak için birçok model ortaya atıldı. Hepsine detaylıca giremeyeceğim bu eter teorileri fazladan bir noktayı daha açıklamaya çalışırken daha da fazla varsayıma ihtiyaç duyuyorlardı.

Bu arada 19. yüzyılın ikinci yarısına geldiğimizde ışığın elektromanyetik dalga teorisi gelişmeye başlamıştı. Fakat herkes Maxwell gibi ışığın bir elektromanyetik dalga olduğuna kolayca ikna olmamıştı. Acaba elektromanyetik dalgalar için de ayrı bir eter mi gerekliydi? Neyse ki 1887-1889 yılları arasında Heinrich Hertz elektromanyetik dalgaların ışıkla birebir aynı olduğunu kanıtladı. Dolayısıyla farklı bir etere daha ihtiyaç kalmadı. Ancak 19. yy sonlarına gelirken ışık saçan eterin sahip olması gereken özellikler artık komik bir hal almıştı:

• Evreni doldurabilmek için katı

• Yüksek frekansları destekleyebilmek için çelikten milyonlarca kat daha sert

• Gezegenlerin hareketini etkilememesi için kütlesiz ve dirençsiz

• Tamamen saydam

• Dağılmaz

• Sıkıştırılamaz

• Çok küçük boyutlarda bile sürekli

olmalıydı.

Tüm bunların yanında çok daha önemli bir nokta vardı. Maxwell denklemlerine göre ışığın hızı etere göre sabit olmalıydı. Daha önce de bahsettiğim üzere o zamanki fiziğe göre bu şaşırtıcı değildi; zira her dalganın hızı yayıldığı homojen ortama göre sabittir. Işığın hızının değişmemesi için eterin evrensel olarak sabit/durağan olması gerekiyordu; aksi halde eterdeki değişime göre ışığın hızı da değişirdi.

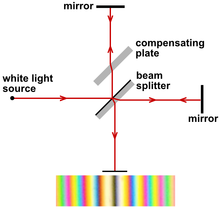
O zaman eter evrensel olarak durağan bir şeyse ve Dünya’mızın da hareket ettiğini biliyorsak eteri saptamamızı sağlayacak bir deney yapabiliriz. Nasıl mı? Görselde gördüğünüz Albert Michelson ve Edward Morley, o zamana kadar yapılmış en hassas deney düzeneğini tasarladılar. Bu deneye göre demet bölücüye bir ışık gönderilecek ve bu ışık iki dik parçaya ayrılacak. Eğer eter Dünya’ya göre hareket ediyorsa iki ışığın farklı zamanlarda geldiğini görmeliyiz. Böylece dünyanın etere göre hızını tespit edebiliriz. Bu deney o zamana kadar yapılmış tüm deneylerden çok daha hassastı ve diğer deneylerden olumlu bir sonuç çıkmasa da bilim camiası bu deneyden bir sonuç çıkmasını bekliyordu. Michelson ve Morley 1887 yılında deneyi yaptılar. Sonuç: Elde var sıfır! İki ışık farklı zamanlarda ulaşmamıştı.

Bu sonucu açıklamak için sürüklenen-eter teorileri ortaya kondu ama hepsi varsayımlar listesine daha da fazla madde ekliyordu. Dikkate değer bir çalışma ise Einsein’ın da gençliğinde çok etkilendiği ve çalışmalarından haberdar olduğu Hendrik Lorentz’den geldi. Lorentz eterin sabit olduğunu, fakat eter içinde ilerleyen nesnelerin bir uzunluk kısalması yaşadığını söyleyerek sonuçları açıklamaya çalıştı. Ayrıca gerçek zaman ve lokal zaman gibi ayrımlardan bahsetse de bunun sadece matematiksel olduğunu ve tabii ki herkes için tek bir zaman olduğunu söyledi.

Her ne kadar sürüklenen eter teorilerinden daha sade ve iyi dursa da Lorentz’in teorisinde de sorunlar vardı. Bir önceki yazımda bahsettiğim üzere 1800’lerin sonuna geldiğimizde fizikte büyük bir kriz durumu hakimdi ve çeşitli çevrelerde ışık çatan eter fikri sorgulanmaya başlamıştı.