Rüzgâr Türbini Aerodinamiği – II

Bir önceki yazıda rüzgâr türbini aerodinamiğine giriş yapmıştık. Bu girişte konuya dair teoriden kısaca bahsedip, sonrasında ise belirli kavramlar üzerinde durulmuştu. Bu yazı, önceki yazının devamı niteliğinde olmakla beraber, türbin kanadı ve aerodinamik performans ilişkisini tartışmayı amaçlamaktadır. Son olarak ise, tartışılan kavramların ilişkisini türbin simülasyon sonuçları ile anlaşılır hale getirilmek istenmektedir.

Daha önce güç, ittirme kuvveti, güç katsayısı gibi temel prensipleri tartışmıştık. Ancak bilinmelidir ki bu kavramlar çok uzun bir işlemin girdileri değil, sonuçlarıdır. Temel olarak, her mühendislik disiplininde olduğu üzere, proje elde edeceği gelire bağlıdır. Ancak bunun anlamı her koşulda maksimum güç elde etmek değildir. Rüzgâr türbinlerinin tasarlanması aşamasında kanatlara pek çok kısıtlama getirilmektedir. Bu kısıtlamalar, proje ömrünün başarıyla tamamlanması ya da projenin yasal sınırlara uyum sağlaması gibi zorunlu kriterlerdir. Yani, tasarım hem maksimum performansı sağlamalıdır, hem de gerçekçi olmak zorundadır. Bu doğrultuda tasarım tekrarlanarak ideal hale getirilmeye çalışılır.

Rüzgâr türbin kanatları günümüzde devasa büyüklüklere ulaşmıştır. Kanat uzunluğu yeni tasarımlarda 120 metrelere ulaşırken, kanat genişliği 7 metrelere ulaşabiliyor. Öyle ki kanadın kök(silindir) kısmında standart boyutlarda basketbol potasını koyup basket oynamak mümkündür. Bu kanatların tasarım aşamasında, getirilen kısıtlamalar ile birlikte maksimum aerodinamik performansını göz önünde bulunduran bir bilgisayar kodu kullanılabilir. Kanat tasarımını farklı bir yazıda bütünü ile tartışmayı istesek de, temel aerodinamiği anlamak için yine de biraz değinmemiz lazım. Kanat genişliği ve kalınlığı kanat üzerinde sürekli değişir ve bununla beraber bu yazıda tartışacağımız kanat profili (Airfoil) de değişir. Figür 1’de kanadın fiziksel özellikleri görülebilir. Ancak en önemlisi sağda ve solda yer alan sayılar ve kanat profil isimleridir.

Figur 1: NREL 5MW Referans Rüzgâr Türbin Kanadı [QBlade][3]

Figürün sol kısmında kanada özgü aerodinamik noktaların uzunluğu verilmiştir (Toplam uzunluk 63 metredir) ve farklı bir not olarak daha önce bahsedilen BEM sistemi, bu noktaların her birini analiz eder. Sağ kısımda ise, her noktaya özgü olarak kullanılan aerodinamik profil verilmiştir. Anlaşılması gereken şu ki, aerodinamik profil kanat boyunca değişir ve bu bize istenilen aerodinamik sonuçları verir. Öncelikle aerodinamik profilin anlaşılması gerekmektedir.

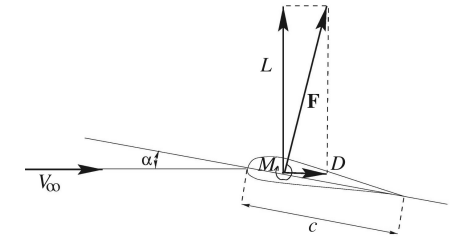
Figür 2: Aerodinamik Profil Üzerindeki Kuvvetler

Figür 2, aerodinamik profilin anlaşılması için idealdir. Şekilde küçük bir kesit görüyoruz, bu aerodinamik profil olarak adlandırılan yapıdır. Görsel olarak akılda canlanması adına küçük bir rüzgâr türbin kanadını elimize aldığımızı düşünebiliriz. Kanadın kök kısmını elimizde, uç kısmını ise yüzümüze doğru tuttuğumuzu varsayalım. Bu pozisyonda, kanadın ortasından kestiğimizde aslında oluşan kesit yukarıda gösterilen aerodinamik profile çok benzeyecektir. Yani aslında rüzgâr türbin kanadı bir aerodinamik profiller bütünüdür. Rüzgâr sonucu kuvvet (Resulting Force) aerodinamik profilde iki farklı kuvvete ayrıştırılır. Bunların ilki kaldırma kuvvetidir (Lift Force). Kaldırma kuvveti, rüzgâr türbinin kendi dönüş yönüne doğru olur ve aslında kinetik enerjinin mekanik enerjiye dönüşmesi bu şekilde olur. Rüzgâr sonucu kuvvetin diğer bileşeni ise sürtünme kuvvetidir (Drag Force). Sürtünme kuvveti, kaldırma kuvvetine dik bir şekilde oluşur ve bilindiği üzere hareketi engelleme yönünde çalışır. Anlaşılacağı üzere, kaldırma kuvveti bizim yararımıza iken, sürtünme kuvveti ise istenmeyen zorunlu bir sonuçtur.

Figür 3: Kaldırma ve Sürtünme Kuvveti Formülleri

Figür 3’te kaldırma ve sürtünme kuvvetlerinin formülleri verilmiştir. Bu denklemlerde:

• ρ (okunuşu rho [Yunan alfabesinden bir harf]) = Hava yoğunluğu

• W = İzafi Hız ( Rüzgâr hızından türbinin dönüş hızı çıkartılarak bulunur. Kanatların gördüğü hız budur.)

• c= Kanat genişliği (Aerodinamik Profil genişliği olarak da adlandırılabilir.)

• C_l= Kaldırma Katsayısı (Lift Coefficient)

• C_d= Sürtünme Katsayısı (Drag Coefficient)

olarak temsil edilir. Temel olarak formüllere bakılırsa ve diğer bütün değişkenlerin sabit tutulduğu var sayılırsa, kaldırma ve sürtünme kuvvetlerinin kanat uzunluğuyla beraber artacağı sonucuna varılabilir. Bunun sebebi ise, kanadın dönüş hızı aynı olsa da yarıçap arttığı için kanadın ucunun hızı, kanatın kökünden daha fazla olacaktır. Ancak burada önemli konu kaldırma ve sürtünme katsayılarıdır ve bunlar rüzgâr türbin kanadı üzerinde değişmektedir.

Kaldırma ve sürtünme katsayıları farklı aerodinamik profiller ve aynı aerodinamik profillerin farklı bağıl kalınlıkları için farklılık gösterir. Bunun sebebi ise farklı aerodinamik profil veya aynı aerodinamik profillerin farklı bağıl kalınlıklarında geometrilerin farklı olmasıdır. Figür 4’te bu görülebilir. Figür 4’te ilk figür NACA olarak gösterilen ile RT-% 30 aerodinamik profilleri farklı dizayn edilmiş profillerdir. Ancak ikinci görselde ise aynı tasarımın farklı bağıl kalınlıklarını görüyoruz. Bağıl kalınlık (Relative Thickness) kalınlığın uzunluğa bölünmesiyle elde edilir.

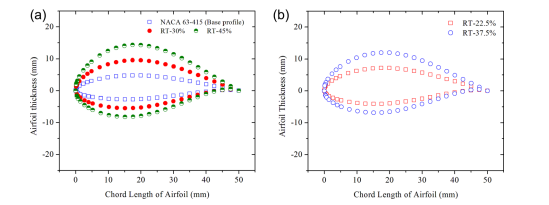
Figür 4: a) Farklı Aerodinamik Profiller b)Aynı Aerodinamik Profil, Farklı Bağıl Kalınlıklar [4]

Aerodinamik profillerin kaldırma ve sürtünme katsayıları simülasyonlar ile elde edilebilir. Ancak akışkanlar mekaniğinin derin konularından biri olduğu için bu konuya bu yazı da değinilmeyecektir. Son olarak aerodinamik profiller için bilinmesi gereken en önemli şeylerden biri ise aynı aerodinamik profilin kaldırma ve sürtünme katsayıları her zaman aynı olmadığıdır. Şöyle ki kaldırma ve sürtünme katsayıları, aerodinamik profilin bir akışkan ( Hava/Rüzgâr) ile etkileşiminden elde edilir. Şimdi bunun deneyini yaptığımızı düşünelim. Elimizde bir aerodinamik profil var ve bunu paralel bir şekilde (0 derece açıyla) bir yere monte edelim. Daha sonra, Figür 2’deki gibi sol tarafından bir rüzgâr gönderdiğimizi düşünelim. Bu durumda, rüzgâr aerodinamik profilin önce ön kenarına (Leading Edge) temas edecek ve ayrılmaya başlayacaktır. Eğer bu rüzgârı görebilseydik, rüzgârın aerodinamik profil etrafından geçip, arka kenarda (Trailing Edge) tekrar birleşmeye başlayacağını görürdük. Bu testi, aerodinamik profili farklı bir açı ile yerleştirdiğimizde tekrarlar ise, rüzgârın davranışının biraz daha farklı olduğunu görebiliriz. Şöyle ki açı değiştiğinde, rüzgâr artık aerodinamik profil üzerine tutunmakta zorlanacaktır. Böylece, aslında kaldırma ve sürtünme değerleri artık o profil için değişmiş olacaktır. Bu test örneği aşağıdaki Figür 5’te görülebilir. 5 derece ve 15 derece ile yerleştirilmiş profiller ve akış çizgileri (Stream Lines), rüzgârın hareketindeki farklılıkları oldukça iyi gösteriyor. Eğer bu sizin ilginizi çeken bir konu ise, internet üzerinde bu terimleri aratarak bu testleri ve simülasyonları izleyebilme şansınız var.

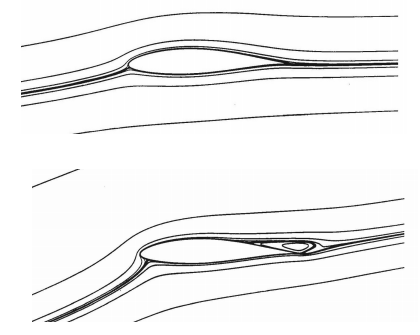
Figür 5: Aerodinamik Profiller 5 ve 15 Derece

Bu yazıda söylediğimiz gibi, sürtünme katsayısı hareketi engelleyici özelliğe sahipken, kaldırma katsayısı ise bizim yararımıza olan bir şey. Böylece diyebiliriz ki, bir kanat yaparken kullandığımız profilin kaldırma katsayısı ne kadar yüksek ve sürtünme katsayısı ne kadar düşük ise aerodinamik performans o kadar yüksek olacaktır. Bilinmesi gerekir ki kanat boyunca bağıl kalınlık azalarak devam eder. Bundan dolayı, aerodinamik profil kanat boyunca değişerek verimli şekilde kullanılmalıdır.

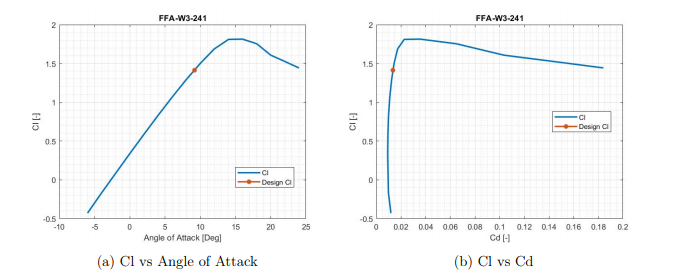
Figür 6: a) Kaldırma Katsayısı ve Açı, b) Kaldırma Katsayısı ve Sürtünme Katsayısı

Figür 6’te ilk grafikte, FFA-W3 adlı aerodinamik profilin % 24.1 bağıl kalınlığına ait verilerini görüyoruz. Bu grafiğe göre, açı arttıkça, belirli bir noktaya kadar kaldırma katsayısı artıyor, bir noktadan sonra ise düşmeye başlıyor. Bu noktaya sapma (Stall) noktası denilir. Bu noktanın niye böyle bir davranış gösterdiğini anlamak için daha önce bahsedilen internet üzerindeki videolar çok yararlı bir kaynaktır. Aynı figürdeki ikinci görselde ise, iki katsayının birbiriyle ilişkisini görüyoruz. Bir noktaya kadar C_l/C_d (Kaldırma Katsayısı/Sürtünme Katsayısı) artarken yine aynı sapma noktasında grafiğin değiştiği görülüyor. Yani, sapma noktasından öncesi ideal bir türbin için oldukça kullanışlı olduğu söylenebilir. Bu iki grafikten çıkarılan sonuç ise, profilin hangi açı ile kanada yerleştirileceğidir.

Konu oldukça karışık olduğu için daha derine inmeyi tercih etmiyoruz. Onun yerine, bu değerler ve daha önceki yazıda kullandığımız değerler arasında ilişki kurulmasına yardımcı olacak simülasyon sonuçlarını değerlendirmenin daha yararlı olacağı kanaatindeyiz.

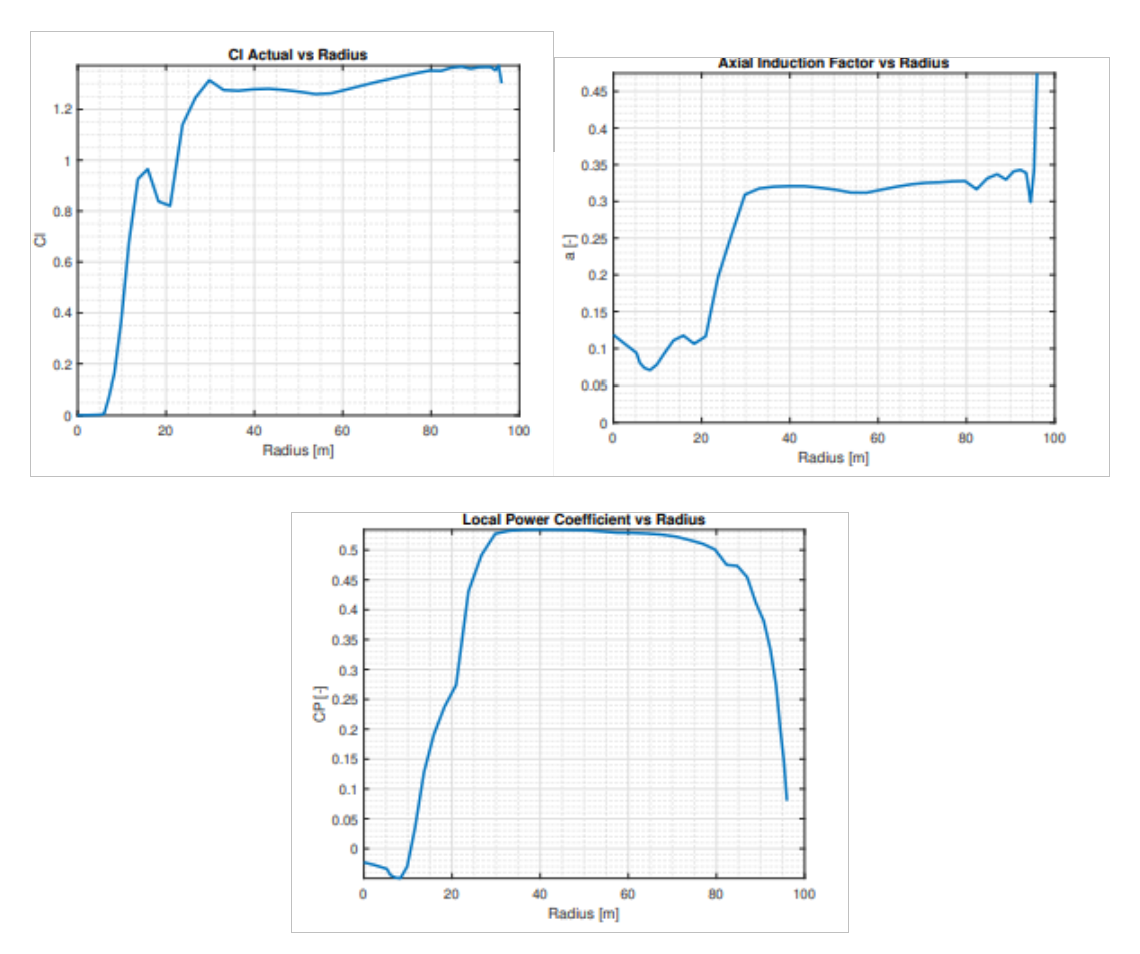
Figür 7: a) Kanat Üzerinde Kaldırma Katsayısı Değerleri, b) Kanat Üzerinde Eksen İndüksiyon Faktörü, c) Kanat Üzerinde Güç Katsayısı

Figür 7, bu değerlerin ilişkisini göstermek için idealdir. Bu sonuçlar, kendi test türbinimden elde ettiğim sonuçlardır ve maalesef bunun için ulaşılabilecek referans veremiyorum. İlk resme baktığımızda kanat üzerinde, kaldırma katsayısının arttığını görmekteyiz. Bunun en büyük sebebi, kanat tasarımında ilk kısım (şekilde ilk 20 metre) aerodinamik performanstan ziyade, yapısal bütünlüğü sağlamak için oldukça verimsiz, ancak yapıyı taşıyacak aerodinamik profiller kullanılmasından dolayıdır. Daha sonrasında bu sayı bir noktaya kadar hızla artar ve daha sonra sabit olarak kanat üzerinde devam eder. Hızlıca artmasının sebebi, aynı tip aerodinamik profillerde bağıl kalınlık düştükçe performans artar (İstisnalar hariç). Böylece, kanatta uç kısımlara gittikçe bağıl kalınlığın düştüğünü de anlayabiliriz. Daha sonra ise, bu kalınlık neredeyse aynıdır ve kaldırma katsayısı da sabit kalır. Buna karşılık, a sayısı da benzer eğilimleri gösterir. Bildiğimiz gibi, a sayısı 0.33 ise kanat oldukça verimlidir. Bu yüzden a sayısı kaldırma katsayısı arttıkça bu 0.33 değerleri etrafında gezinir. Not olarak, en sonra a sayısının aşırı yükseldiğini görmekteyiz. Bu aşırı yükseliş önemsenmemelidir. Çünkü bu teori kaynaklı bir yanlışlıktan ibarettir. Son olarak güç katsayısını görmekteyiz. Güç katsayısı bir türbin için tek bir sayı olmakla birlikte, kanat üzerinde de gözlemlenebilir. Genel olarak yine aynı ilişki görülmekle beraber, sondaki düşüş, a sayısından gelen teorik yanlışlığı simgeler. Bu türbin için genel güç katsayısı % 47.28 olarak elde edilmiştir.

Oldukça karışık bir konuyu elimizden geldiği kadar sadeleştirerek anlatmaya çalıştık. Umuyoruz ki gayet anlaşılır ve kolay okunabilir bir yazı olmuştur ve sizler için de merak uyandırmayı başarmıştır. Önümüzdeki yazılarda yine daha öncekiler gibi rüzgâr türbinleri için teknik konuları sadeleştirmeye ve örnekler vererek anlatmaya çalışacağız.

Kaynakça

1. Hansen, M. O. L. (2015). Aerodynamics of wind turbines. (3 ed.) Earthscan

2. Bak, C. (2013). Aerodynamic design of wind turbine rotors. In P. Brøndsted, & R. Nijssen (Eds.), Advances in wind turbine blade design and materials Woodhead Publishing. Woodhead Publishing Series in Energy, No. 47

3. Jonkman, J, Butterfield, S., Musial, W., and Scott, G., “Definition of a 5-MW Reference Wind Turbine for Offshore System Development,” NREL/TP-500-38060, Golden, CO: National Renewable Energy Laboratory, February 2009.

4. Mazarbhuiya, H. M. S. M., A. Biswas, and K. K. Sharma. 2018.Performance Investigations of Modified Asymmetric BladeH-Darrieus VAWT Rotors. Journal of Renewable and Sustainable Energy 033302